Persamaan dan Fungsi Kuadrat

Persamaan kuadrat satu variabel adalah suatu persamaan yang pangkat tertingginya dua. Secara umum, bentuk persamaan kuadrat adalah ax2  + bx + c = 0 dengan a ≠ 0, a, b, c ∈ R. Konstanta a, b, c pada persamaan ini disebut sebagai koefisien. Beberapa contoh persamaan kuadrat yaitu: 3x2  – 7x + 5 = 0, x2  – x + 12 = 0, x2  – 9 = 0, 2x(x – 7)= 0 dan lainnya.

 Akar persamaan kuadrat dari ax2   + bx + c = 0 adalah nilai x yang memenuhi persamaan tersebut. Cara menentukan akar persamaan kuadrat ada tiga cara, yaitu:

 (1)   Memfaktorkan

 (2)   Melengkapi Kuadrat Sempurna

 (3)   Rumus Kuadratik (Rumus abc)

 Dalam hal ini rumus kuadratik (Rumus abc) adalah

Karakteristik  dari  akar-akar  persamaan  kuadrat  dapat  dilihat  dari  koefisen persamaannya. Berikut karakteristik-karakteristik dari persamaan kuadrat berdasarkan koefisien-koefisien persamaan kuadratnya:

         

Misal suatu persamaan kuadrat ax2   + bx + c = 0 dengan nilai diskriminannya adalah D = b2 – 4ac maka untuk D < 0 persamaan kuadrat tidak mempunyai akar- akar, D = 0 persamaan kuadrat mempunyai akar-akar kembar, D > 0 persamaan kuadrat mempunyai dua akar berbeda.

Grafik Fungsi Kuadrat

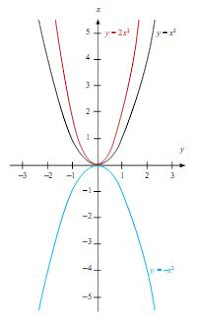
Fungsi kuadrat merupakan fungsi yang berbentuk y = ax2   + bx + c, dengan a ≠ 0.

Grafik  dari  fungsi  kuadrat  menyerupai  parabola,  sehingga  dapat  dikatakan juga sebagai fungsi parabola

.

Menentukan Sumbu Simetri dan Titik Optimum

Langkah-langkah mensketsa grafik fungsi kuadrat :

Langkah 1   :  Menentukan bentuk parabola (terbuka ke atas atau ke bawah).

Langkah 2    :  Menentukan perpotongan grafik terhadap sumbu-x; yaitu, koordinat titik potongnya adalah (x , 0) yang memenuhi persamaan f(x) = 0

Langkah 3   :  Menentukan perpotongan grafik terhadap sumbu-y; yaitu, koordinat titik potongnya adalah (0 , y1) dengan y1 didapatkan berdasarkan persamaan y1 = f(0)

Langkah 4   :  Menentukan sumbu simetri dan nilai optimum dari grafik fungsi

Langkah 5   :  Mensketsa grafik fungsi kuadrat berdasarkan langkah (1), (2), (3), dan (4).

Menentukan Fungsi Kuadrat

Untuk menentukan  fungsi  kuadrat  diperlukan  beberapa  informasi,  di  antaranya sebagai berikut.

 1.     Beberapa titik koordinat yang dilalui fungsi kuadrat tersebut.

 2.     Titik potong fungsi kuadrat tersebut di sumbu-x.

 3.     Titik potong fungsi kuadrat tersebut di sumbu-y.

 4.     Titik puncak dan sumbu simetri.

Aplikasi Fungsi Kuadrat

Berikut langkah-langkah untuk menyelesaikan masalah optimalisasi fungsi kuadrat.

Langkah 1.  Tentukan variabel yang akan dioptimalisasi yaitu y dan variabel yang bebas yaitu x.

Langkah 2.  Jika model y = ax2    + bx + c tidak diketahui maka bentuklah model

y = ax2  + bx + c dari permasalahan.

Langkah 3.  Tentukan nilai optimum dari model yang didapatkan pada Langkah 2.

Sumber : Buku Guru BSE Matematika kelas 9 edisi revisi 2018

#hari #klikhari #pakhari #spenduta #sobatspenduta #spendutasidoarjo #smpn2taman #smpn2tamansidoarjo #smp2taman #smp2tamansidoarjo #banggaspenduta

Read More

Perpangkatan dan Bentuk Akar

1. Bilangan Berpangkat 

Perpangkatan adalah perkalian berulang dari suatu bilangan yang sama. Bentuk umum dari perpangkatan adalah

dengan n bilangan bulat positif sebanyak n

Contoh, perpangkatan 3 seperti di bawah ini:

3 × 3 × 3 × 3 × 3 = 35

35  adalah perpangkatan 3.

3 disebut sebagai bilangan pokok (basis) sedangkan 5 sebagai pangkat (eksponen).

2. Perkalian pada Perpangkatan

Hasil kali dari perpangkatan dengan basis yang sama Sifat perkalian dalam perpangkatan: am  × an  = am + n Contoh: 32  × 33  = 32 + 3 = 35

Hasil pemangkatan dari perpangkatan dengan basis yang sama Sifat pemangkatan pada perpangkatan: (am)n  = am ∙ n = amn Contoh: (32)3  = 32∙3  = 36

Hasil perpangkatan dari suatu perkalian bilangan

Sifat perpangkatan dari perkalian bilangan:  (a∙b)m  = ambm

Contoh: (2∙3)3  = 23∙33

3. Pembagian pada Perpangkatan

Hasil bagi dari perpangkatan dengan basis yang sama

Perpangkatan pada pecahan

4. Pangkat Nol, Pangkat Negatif, dan Bentuk Akar

PANGKAT NOL

Untuk setiap a bilangan real tak nol, a0  bernilai 1

Secara aljabar dapat ditulis kembali sebagai berikut:

a0  = 1  untuk a bilangan real dan a ≠ 0

PANGKAT NEGATIF

      Untuk setiap a bilangan real tak nol dan n bilangan bulat, berlaku:

 BENTUK AKAR

Menyederhanakan perkalian Bentuk Akar

5. Notasi Ilmiah

 Notasi ilmiah (bentuk baku) dari suatu bilangan positif dituliskan dalam bentuk

a × 10n  dengan  ...  1 < a < 10 ... dan n adalah bilangan bulat.

Misalkan notasi ilmiah untuk 2.300 adalah

Contoh:

8.500.000 = 8,5 × 1.000.000 = 8,5 × 106

144.000.000 = 1,44 × 100.000.000 = 1,44 × 108

Bilangan antara 0 dan 1

Gunakan pangkat negatif ketika kamu memindahkan titik desimal ke kanan.

Contoh:

0,0000085 = 8,5 : 1.000.000 = 8,5 × 10–6

0,0000000144 = 1,44 : 100.000.000 = 1,44 × 10–8

Sumber : Buku Guru BSE Matematika Kelas 9 Edisi Revisi 2018

#hari #klikhari #pakhari #spenduta #sobatspenduta #spendutasidoarjo #smpn2taman #smpn2tamansidoarjo #smp2taman #smp2tamansidoarjo #banggaspenduta

Read More