Bangun Ruang Sisi Lengkung

1. TABUNG
Tabung adalah bangun ruang sisi lengkung yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki tiga sisi yakni dua sisi datar dan satu sisi lengkung.

 Benda-benda dalam kehidupan sehari-hari yang menyerupai tabung adalah tong sampah, kaleng susu, lilin, dan pipa.

Luas Tabung

Luas  tabung   ekuivalen   dengan   jumlahan   semua luas bangun penyusun dari jaring-jaring tabung. Jaring-jaring tabung terdiri atas dua lingkaran dan satu persegi panjang.

Misalkan terdapat tabung dengan jari jari r dan tinggi t, maka:

L  =  Luas jaring-jaring tabung

       = 2 × Luas Lingkaran + Luas ABCD  (Ingat: panjang AB = keliling lingkaran)

           = 2πr2  + AB × BC                                                 panjang BC = tinggi tabung.

      = 2πr2  + 2πr × t

      = 2πr(r + t)

Volume Tabung

Volume tabung adalah hasil perkalian dari luas alas tabung  dengan  tinggi  tabung  atau  dapat  dirumuskan sebagai berikut:

V =  L  × t

    = πr2  × t

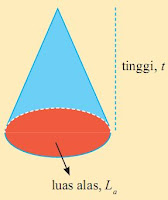
2.  KERUCUT

Kerucut adalah bangun ruang sisi lengkung yang dapat dibentuk dari  tabung dengan mengubah tutup tabung menjadi titik. Titik tersebut biasanya disebut dengan titik puncak. Kerucut memiliki dua sisi, yaitu  satu sisi datar dan satu sisi lengkung. Kerucut merupakan limas dengan alas lingkaran.

Benda-benda dalam kehidupan sehari-hari yang menyerupai kerucut adalah topi ulang tahun, topi petani, dan cone es krim

Luas Permukaan Kerucut

Luas  permukaan  ekuivalen  dengan  jumlahan semua  luas   bangun   penyusun   dari   jaring-jaring kerucut.   Jaring-jaring   kerucut   terdiri   atas   satu lingkaran dan satu selimut yang berbentuk juring.

Misalkan terdapat kerucut dengan jari jari r dan garis pelukis s, maka:

L =  Luas Lingkaran + Luas Juring ABC

   = πr2  + πrs

   = πr(r + s)

Volume Kerucut

Volume kerucut adalah 1/3 bagian dari volume tabung dengan jari-jari dan tinggi yang sama atau dapat dirumuskan sebagai berikut:

3. BOLA

Bola adalah bangun ruang sisi lengkung yang dibentuk dari tak hingga lingkaran yang memiliki jari-jari sama panjang dan berpusat pada titik yang sama. Bola hanya memiliki  satu sisi yang merupakan sisi lengkung. Bola dapat dibentuk dengan memutar/merotasi setengah lingkaran sebesar 360o dengan diameter sebagai sumbu rotasi

Benda dalam kehidupan sehari-hari yang berbentuk bola adalah bola olah raga (sepak bola, basket, voli dan lain-lain), kelereng, globe, dan lainnya.

Luas Permukaan Bola

Luas permukaan bola adalah sama dengan 4 kali luas lingkaran  yang  memiliki  jari-jari  yang  sama  atau  dapat dituliskan sebagai berikut

              L = 4πr2   

Volume Bola

#hari #klikhari #pakhari #spenduta #sobatspenduta #spendutasidoarjo #smpn2taman #smpn2tamansidoarjo #smp2taman #smp2tamansidoarjo #banggaspenduta

Read More

Kekongruenan dan Kesebangunan

Syarat Dua Bangun Datar Kongruen
Dua bangun yang mempunyai bentuk dan ukuran yang sama dinamakan kongruen. Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu:

 (i)    sisi-sisi yang bersesuaian sama panjang, dan

 (ii)   sudut-sudut yang bersesuaian sama besar.

Syarat Dua Segitiga Kongruen

Dua  bangun  yang  mempunyai  bentuk  dan  ukuran  yang  sama  dinamakan kongruen. Dua segitiga dikatakan kongruen jika hanya jika memenuhi syarat berikut ini:

 (i)    sisi-sisi yang bersesuaian sama panjang

 (ii)   sudut-sudut yang bersesuaian sama besar.

Untuk menguji apakah dua segitiga kongruen atau tidak, tidak perlu menguji semua pasangan sisi dan sudut yang bersesuaian. Dua segitiga dikatakan kongruen jika memenuhi salah satu kondisi berikut ini:

1.     Ketiga pasangan sisi yang bersesuaian sama panjang. Biasa disebut dengan kriteria sisi – sisi – sisi.

 2.     Dua pasang sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar. Biasa disebut dengan kriteria sisi – sudut  – sisi.

3.     Dua pasang sudut yang bersesuaian sama besar dan sisi yang menghubungkan kedua sudut tersebut sama panjang. Biasa disebut dengan kriteria sudut – sisi –sudut.

4.    Dua  pasang  sudut  yang  bersesuaian  sama  besar  dan  sepasang  sisi  yang bersesuaian sama panjang. Biasa disebut dengan kriteria sudut – sudut – sisi.

5.    Khusus untuk segitiga siku-siku, sisi miring dan satu sisi siku yang bersesuaian sama panjang.

Kesebangunan Bangun Datar

Dua bangun datar yang mempunyai bentuk yang sama disebut sebangun. Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan. Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat: 

(i)    perbandingan panjang sisi yang bersesuaian senilai

(ii)   sudut yang bersesuaian besarnya sama

Kesebangunan Dua Segitiga

Dua segitiga dikatakan sebangun jika hanya jika memenuhi syarat berikut ini. 

(i)    Perbandingan sisi-sisi yang bersesuaian senilai.

(ii)   Besar sudut-sudut yang bersesuaian sama.

Syarat Dua Segitiga Sebangun

Dua segitiga dikatakan sebangun,  jika memenuhi salah satu kondisi berikut ini.

1.         Perbandingannya ketiga pasangan sisi yang bersesuaian sama

2.         Dua pasang sudut yang bersesuaian sama besar

3.     Perbandingan dua pasang sisi yang bersesuaian sama dan sudut yang diapitnya sama besar.

Kesebangunan Khusus dalam Segitiga Siku-siku

#hari #klikhari #pakhari #spenduta #sobatspenduta #spendutasidoarjo #smpn2taman #smpn2tamansidoarjo #smp2taman #smp2tamansidoarjo #banggaspenduta

Read More